浅层神经网络

一、多层感知机与反向传播算法

#

1.1 单层感知机的问题

#

单层感知机（Rosenblatt）可以实现简单的分类问题，但不能解决异或问题。（异或逻辑运算从几何意义上讲是线性不可分的）
MLP引入了隐藏层，和非线性激活函数，被证明具有通用逼近能力。MLP的基本结构如下图所示，其中每一个小球就代表一个神经元结构。

图片来源：MLP的理解（CSDN）

1.2 基本BP算法

#

1.2.1 权值确定方法

#

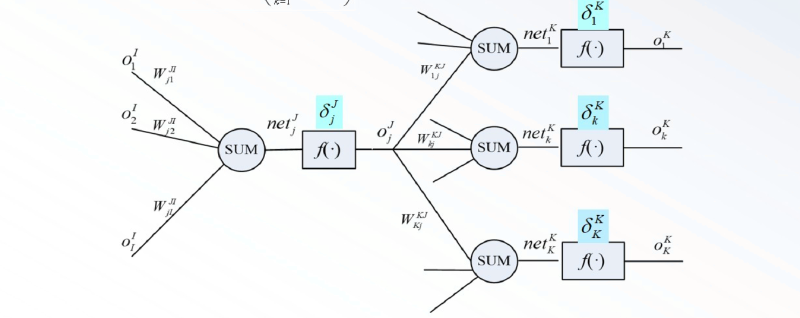
在某种最优准则下，通过学习确定网络的权值$W_{kj}^{KJ}$和$W_{ji}^{JI}$。
有网络输出为：$o_k^K=f(net_k^K)$； 累加器输出为：$net_k^K=\sum\limits_{j=1}^{J}W_{kj}^{KJ}\cdot+o_j^J+b_k^K$
定义损失函数：$E=\frac{1}{2} \sum\limits_{k=1}^K\left(d_k-o_k^K\right)^2$
其中，$d_k$为输出层第k个神经元的期望输出，$o_k^K$为该神经元的实际输出。

后一个神经元与前一个神经元权值的关系如下，难点在于求出其中的微分项。

$$\begin{cases} W_{k j}^{K J}(n+1)=W_{k j}^{K J}(n)-\eta_k\left(\frac{\partial E}{\partial W_{k j}^{K J}}\right) \\ W_{j i}^{J I}(n+1)=W_{j i}^{J I}(n)-\eta_j\left(\frac{\partial E}{\partial W_{j i}^{J I}}\right) \end{cases}$$

根据以上式子，由链式求导法则可得：

$$\begin{cases} -\frac{\partial E}{\partial W_{k j}^{K J}}=\left(d_k-O_k^K\right) f^{\prime}\left(n e t_k^K\right) \cdot O_j^J\\ -\frac{\partial E}{\partial W_{j i}^{J I}}=\sum_{k=1}^K\left(d_k-O_k^K\right) f^{\prime}\left(n e t_k^K\right) W_{k j}^{K J} f^{\prime}\left(n e t_j^J\right) O_i^I \end{cases}$$

两式对照可得，本层误差信号 = 下一层误差信号累加和 * 本层激励函数的导数。
定义输出层第k个神经元的误差信号：$\delta_k=-\frac{\partial E}{\partial n e t_k^K}=\left(d_k-O_k^K\right)f^{\prime}\left(n e t_k^K\right)$
（误差信号的形式由激活函数决定）
隐含层第j个神经元的误差信号为：$\delta_j=-\frac{\partial E}{\partial n e t_j^J}$
将$\delta_k$带入$-\frac{\partial E}{\partial W_{k j}^{K J}}$，再带入$W_{k j}^{K J}(n+1)$，得到

$$\begin{aligned} & W_{k j}^{K J}(n+1)=W_{k j}^{K J}(n)+\eta_k \cdot\delta_k\cdot O_j^J \\ & k=1,2 \cdots K ; j=1,2 \cdots J\end{aligned}$$

有

$$\begin{aligned}&\delta_{k}=-\frac{\partial E}{\partial net_{k}^{K}};{\frac{\partial net_{k}^{K}}{\partial O_{j}^{J}}=W_{kj}^{KJ}}\\&\frac{\partial O_{j}^{J}}{\partial net_{j}^{J}}=f^{^{\prime}}(net_{j}^{J});{\frac{\partial net_{j}^{J}}{\partial W_{ji}^{JI}}=O_{i}^{I}}\end{aligned}$$

对于隐含层：

$$\begin{aligned}\delta_{j}&=-\frac{\partial E}{\partial net_{j}^{J}}=-\sum_{k=1}^{K}\left(\frac{\partial E}{\partial net_{k}^{K}}\right)\frac{\partial net_{k}^{K}}{\partial O_{i}^{J}}\frac{\partial O_{j}}{\partial net_{j}^{J}}\\&=f^{^{\prime}}(net_{j}^{J})\left(\sum_{k=1}^{K}\delta_{k}W_{kj}^{KJ}\right)\end{aligned}$$

在MLP网络中，误差是反向传播的，于是

$$\begin{aligned}-\frac{\partial E}{\partial W_{ji}^{JI}}=&\left(-\sum_{k=1}^{K}\frac{\partial E}{\partial net_{k}^{K}}\bullet\frac{\partial net_{k}^{K}}{\partial O_{j}^{J}}\bullet\frac{\partial O_{j}^{J}}{\partial net_{j}^{J}}\right)\bullet\frac{\partial net_{j}^{J}}{\partial W_{ji}^{JI}}\\&=\delta_{j}\bullet O_{i}^{I}\end{aligned}$$

1.2.2 核心内容总结

#

输出层学习算法：

$$\begin{aligned}&W_{kj}^{KJ}(n+1)=W_{kj}^{KJ}(n)+\eta_{k}\cdot\delta_{k}\cdot O_{j}^{J}\\&k=1,2,\cdots,K;j=1,2,\cdots,J\\&\delta_{k}=(d_{k}-O_{k}^{K})f^{\prime}\left(net_{k}^{K}\right)\end{aligned}$$

隐含层学习算法：

$$\begin{aligned}&W_{ji}^{JI}(n+1)=W_{ji}^{JI}(n)+\eta_{j}\cdot\delta_j\cdot O_{i}^{I}\\&i=1,2,\cdots,I;j=1,2,\cdots,J\\&\delta_{j}=f^{^{\prime}}(net_{j}^{J})\left(\sum_{k=1}^{K}\delta_{k}W_{kj}^{KJ}\right)\end{aligned}$$

1.2.3 BP算法的特点

#

• 工作信号正向传播。在信号的向后传递过程中网络的权值是固定不变的，每一层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出，则转入误差信号反向传输。
• 误差从后往前传播。误差信号由输出层开始逐层向前传播，在反向传播 的过程中，网络的权值由误差反馈进行调节，通过权值的不断修正使网 络的实际输出更接近期望输出。
• 并行的：硬件实现速度快
• 层内无神经元连接

二、径向基函数RBF网络

#

三、概率PRBF神经网络

#

四、动态神经网络

#

通过邮件回复